Friday, 5 June 2015

Statistics

An important area of enquiry is how accurate, and authentic statistics are. With the UDP a set of them could be scrutinized rigorously. RS



From Wikipedia, the free encyclopedia/ Blogger Ref Link http://www.p2pfoundation.net/Universal_Debating_Project

Jump to: navigation, search


More probability density is found as one gets closer to the expected (mean) value in a normal distribution. Statistics used in standardized testing assessment are shown. The scales include standard deviations, cumulative percentages, percentile equivalents, Z-scores, T-scores, standard nines, and percentages in standard nines.


Scatter plots are used in descriptive statistics to show the observed relationships between different variables.
Statistics is the study of the collection, analysis, interpretation, presentation, and organization of data.[1] In applying statistics to, e.g., a scientific, industrial, or societal problem, it is conventional to begin with a statistical population or a statistical model process to be studied. Populations can be diverse topics such as "all persons living in a country" or "every atom composing a crystal". Statistics deals with all aspects of data including the planning of data collection in terms of the design of surveys and experiments.[1]
When census data cannot be collected, statisticians collect data by developing specific experiment designs and survey samples. Representative sampling assures that inferences and conclusions can safely extend from the sample to the population as a whole. An experimental study involves taking measurements of the system under study, manipulating the system, and then taking additional measurements using the same procedure to determine if the manipulation has modified the values of the measurements. In contrast, an observational study does not involve experimental manipulation.
Two main statistical methodologies are used in data analysis: descriptive statistics, which summarizes data from a sample using indexes such as the mean or standard deviation, and inferential statistics, which draws conclusions from data that are subject to random variation (e.g., observational errors, sampling variation).[2] Descriptive statistics are most often concerned with two sets of properties of a distribution (sample or population): central tendency (or location) seeks to characterize the distribution's central or typical value, while dispersion (or variability) characterizes the extent to which members of the distribution depart from its center and each other. Inferences on mathematical statistics are made under the framework of probability theory, which deals with the analysis of random phenomena. To make an inference upon unknown quantities, one or more estimators are evaluated using the sample.
Standard statistical procedure involve the development of a null hypothesis, a general statement or default position that there is no relationship between two quantities. Rejecting or disproving the null hypothesis is a central task in the modern practice of science, and gives a precise sense in which a claim is capable of being proven false. What statisticians call an alternative hypothesis is simply an hypothesis that contradicts the null hypothesis. Working from a null hypothesis two basic forms of error are recognized: Type I errors (null hypothesis is falsely rejected giving a "false positive") and Type II errors (null hypothesis fails to be rejected and an actual difference between populations is missed giving a "false negative"). A critical region is the set of values of the estimator that leads to refuting the null hypothesis. The probability of type I error is therefore the probability that the estimator belongs to the critical region given that null hypothesis is true (statistical significance) and the probability of type II error is the probability that the estimator doesn't belong to the critical region given that the alternative hypothesis is true. The statistical power of a test is the probability that it correctly rejects the null hypothesis when the null hypothesis is false. Multiple problems have come to be associated with this framework: ranging from obtaining a sufficient sample size to specifying an adequate null hypothesis.[citation needed]
Measurement processes that generate statistical data are also subject to error. Many of these errors are classified as random (noise) or systematic (bias), but other important types of errors (e.g., blunder, such as when an analyst reports incorrect units) can also be important. The presence of missing data and/or censoring may result in biased estimates and specific techniques have been developed to address these problems. Confidence intervals allow statisticians to express how closely the sample estimate matches the true value in the whole population. Formally, a 95% confidence interval for a value is a range where, if the sampling and analysis were repeated under the same conditions (yielding a different dataset), the interval would include the true (population) value in 95% of all possible cases. In statistics, dependence is any statistical relationship between two random variables or two sets of data. Correlation refers to any of a broad class of statistical relationships involving dependence. If two variables are correlated, they may or may not be the cause of one another. The correlation phenomena could be caused by a third, previously unconsidered phenomenon, called a lurking variable or confounding variable.
Statistics can be said to have begun in ancient civilization, going back at least to the 5th century BC, but it was not until the 18th century that it started to draw more heavily from calculus and probability theory. Statistics continues to be an area of active research, for example on the problem of how to analyze Big data.

Scope[edit]

Statistics is a mathematical body of science that pertains to the collection, analysis, interpretation or explanation, and presentation of data,[3] or as a branch of mathematics.[4] Some consider statistics to be a distinct mathematical science rather than a branch of mathematics.[vague][5][6]

Mathematical statistics[edit]

Main article: Mathematical statistics
Mathematical statistics is the application of mathematics to statistics, which was originally conceived as the science of the state — the collection and analysis of facts about a country: its economy, land, military, population, and so forth. Mathematical techniques used for this include mathematical analysis, linear algebra, stochastic analysis, differential equations, and measure-theoretic probability theory.[7][8]

Overview[edit]

In applying statistics to e.g. a scientific, industrial, or societal problem, it is necessary to begin with a population or process to be studied. Populations can be diverse topics such as "all persons living in a country" or "every atom composing a crystal".
Ideally, statisticians compile data about the entire population (an operation called census). This may be organized by governmental statistical institutes. Descriptive statistics can be used to summarize the population data. Numerical descriptors include mean and standard deviation for continuous data types (like income), while frequency and percentage are more useful in terms of describing categorical data (like race).
When a census is not feasible, a chosen subset of the population called a sample is studied. Once a sample that is representative of the population is determined, data is collected for the sample members in an observational or experimental setting. Again, descriptive statistics can be used to summarize the sample data. However, the drawing of the sample has been subject to an element of randomness, hence the established numerical descriptors from the sample are also due to uncertainty. To still draw meaningful conclusions about the entire population, inferential statistics is needed. It uses patterns in the sample data to draw inferences about the population represented, accounting for randomness. These inferences may take the form of: answering yes/no questions about the data (hypothesis testing), estimating numerical characteristics of the data (estimation), describing associations within the data (correlation) and modeling relationships within the data (for example, using regression analysis). Inference can extend to forecasting, prediction and estimation of unobserved values either in or associated with the population being studied; it can include extrapolation and interpolation of time series or spatial data, and can also include data mining.

Data collection[edit]

Sampling[edit]

In case census data cannot be collected, statisticians collect data by developing specific experiment designs and survey samples. Statistics itself also provides tools for prediction and forecasting the use of data through statistical models. To use a sample as a guide to an entire population, it is important that it truly represent the overall population. Representative sampling assures that inferences and conclusions can safely extend from the sample to the population as a whole. A major problem lies in determining the extent that the sample chosen is actually representative. Statistics offers methods to estimate and correct for any random trending within the sample and data collection procedures. There are also methods of experimental design for experiments that can lessen these issues at the outset of a study, strengthening its capability to discern truths about the population.
Sampling theory is part of the mathematical discipline of probability theory. Probability is used in "mathematical statistics" (alternatively, "statistical theory") to study the sampling distributions of sample statistics and, more generally, the properties of statistical procedures. The use of any statistical method is valid when the system or population under consideration satisfies the assumptions of the method. The difference in point of view between classic probability theory and sampling theory is, roughly, that probability theory starts from the given parameters of a total population to deduce probabilities that pertain to samples. Statistical inference, however, moves in the opposite direction—inductively inferring from samples to the parameters of a larger or total population.

Experimental and observational studies[edit]

A common goal for a statistical research project is to investigate causality, and in particular to draw a conclusion on the effect of changes in the values of predictors or independent variables on dependent variables or response. There are two major types of causal statistical studies: experimental studies and observational studies. In both types of studies, the effect of differences of an independent variable (or variables) on the behavior of the dependent variable are observed. The difference between the two types lies in how the study is actually conducted. Each can be very effective. An experimental study involves taking measurements of the system under study, manipulating the system, and then taking additional measurements using the same procedure to determine if the manipulation has modified the values of the measurements. In contrast, an observational study does not involve experimental manipulation. Instead, data are gathered and correlations between predictors and response are investigated. While the tools of data analysis work best on data from randomized studies, they are also applied to other kinds of data – like natural experiments and observational studies[9] – for which a statistician would use a modified, more structured estimation method (e.g., Difference in differences estimation and instrumental variables, among many others) that produce consistent estimators.

Experiments[edit]

The basic steps of a statistical experiment are:
  1. Planning the research, including finding the number of replicates of the study, using the following information: preliminary estimates regarding the size of treatment effects, alternative hypotheses, and the estimated experimental variability. Consideration of the selection of experimental subjects and the ethics of research is necessary. Statisticians recommend that experiments compare (at least) one new treatment with a standard treatment or control, to allow an unbiased estimate of the difference in treatment effects.
  2. Design of experiments, using blocking to reduce the influence of confounding variables, and randomized assignment of treatments to subjects to allow unbiased estimates of treatment effects and experimental error. At this stage, the experimenters and statisticians write the experimental protocol that will guide the performance of the experiment and which specifies the primary analysis of the experimental data.
  3. Performing the experiment following the experimental protocol and analyzing the data following the experimental protocol.
  4. Further examining the data set in secondary analyses, to suggest new hypotheses for future study.
  5. Documenting and presenting the results of the study.
Experiments on human behavior have special concerns. The famous Hawthorne study examined changes to the working environment at the Hawthorne plant of the Western Electric Company. The researchers were interested in determining whether increased illumination would increase the productivity of the assembly line workers. The researchers first measured the productivity in the plant, then modified the illumination in an area of the plant and checked if the changes in illumination affected productivity. It turned out that productivity indeed improved (under the experimental conditions). However, the study is heavily criticized today for errors in experimental procedures, specifically for the lack of a control group and blindness. The Hawthorne effect refers to finding that an outcome (in this case, worker productivity) changed due to observation itself. Those in the Hawthorne study became more productive not because the lighting was changed but because they were being observed.[10]

Observational study[edit]

An example of an observational study is one that explores the correlation between smoking and lung cancer. This type of study typically uses a survey to collect observations about the area of interest and then performs statistical analysis. In this case, the researchers would collect observations of both smokers and non-smokers, perhaps through a case-control study, and then look for the number of cases of lung cancer in each group.

Types of data[edit]

Main articles: Statistical data type and Levels of measurement
Various attempts have been made to produce a taxonomy of levels of measurement. The psychophysicist Stanley Smith Stevens defined nominal, ordinal, interval, and ratio scales. Nominal measurements do not have meaningful rank order among values, and permit any one-to-one transformation. Ordinal measurements have imprecise differences between consecutive values, but have a meaningful order to those values, and permit any order-preserving transformation. Interval measurements have meaningful distances between measurements defined, but the zero value is arbitrary (as in the case with longitude and temperature measurements in Celsius or Fahrenheit), and permit any linear transformation. Ratio measurements have both a meaningful zero value and the distances between different measurements defined, and permit any rescaling transformation.
Because variables conforming only to nominal or ordinal measurements cannot be reasonably measured numerically, sometimes they are grouped together as categorical variables, whereas ratio and interval measurements are grouped together as quantitative variables, which can be either discrete or continuous, due to their numerical nature. Such distinctions can often be loosely correlated with data type in computer science, in that dichotomous categorical variables may be represented with the Boolean data type, polytomous categorical variables with arbitrarily assigned integers in the integral data type, and continuous variables with the real data type involving floating point computation. But the mapping of computer science data types to statistical data types depends on which categorization of the latter is being implemented.
Other categorizations have been proposed. For example, Mosteller and Tukey (1977)[11] distinguished grades, ranks, counted fractions, counts, amounts, and balances. Nelder (1990)[12] described continuous counts, continuous ratios, count ratios, and categorical modes of data. See also Chrisman (1998),[13] van den Berg (1991).[14]
The issue of whether or not it is appropriate to apply different kinds of statistical methods to data obtained from different kinds of measurement procedures is complicated by issues concerning the transformation of variables and the precise interpretation of research questions. "The relationship between the data and what they describe merely reflects the fact that certain kinds of statistical statements may have truth values which are not invariant under some transformations. Whether or not a transformation is sensible to contemplate depends on the question one is trying to answer" (Hand, 2004, p. 82).[15]

Terminology and theory of inferential statistics[edit]

Statistics, estimators and pivotal quantities[edit]

Consider an independent identically distributed (IID) random variables with a given probability distribution: standard statistical inference and estimation theory defines a random sample as the random vector given by the column vector of these IID variables.[16] The population being examined is described by a probability distribution that may have unknown parameters.
A statistic is a random variable that is a function of the random sample, but not a function of unknown parameters. The probability distribution of the statistic, though, may have unknown parameters.
Consider now a function of the unknown parameter: an estimator is a statistic used to estimate such function. Commonly used estimators include sample mean, unbiased sample variance and sample covariance.
A random variable that is a function of the random sample and of the unknown parameter, but whose probability distribution does not depend on the unknown parameter is called a pivotal quantity or pivot. Widely used pivots include the z-score, the chi square statistic and Student's t-value.
Between two estimators of a given parameter, the one with lower mean squared error is said to be more efficient. Furthermore, an estimator is said to be unbiased if its expected value is equal to the true value of the unknown parameter being estimated, and asymptotically unbiased if its expected value converges at the limit to the true value of such parameter.
Other desirable properties for estimators include: UMVUE estimators that have the lowest variance for all possible values of the parameter to be estimated (this is usually an easier property to verify than efficiency) and consistent estimators which converges in probability to the true value of such parameter.
This still leaves the question of how to obtain estimators in a given situation and carry the computation, several methods have been proposed: the method of moments, the maximum likelihood method, the least squares method and the more recent method of estimating equations.

Null hypothesis and alternative hypothesis[edit]

Interpretation of statistical information can often involve the development of a null hypothesis in that the assumption is that whatever is proposed as a cause has no effect on the variable being measured.
The best illustration for a novice is the predicament encountered by a jury trial. The null hypothesis, H0, asserts that the defendant is innocent, whereas the alternative hypothesis, H1, asserts that the defendant is guilty. The indictment comes because of suspicion of the guilt. The H0 (status quo) stands in opposition to H1 and is maintained unless H1 is supported by evidence "beyond a reasonable doubt". However, "failure to reject H0" in this case does not imply innocence, but merely that the evidence was insufficient to convict. So the jury does not necessarily accept H0 but fails to reject H0. While one can not "prove" a null hypothesis, one can test how close it is to being true with a power test, which tests for type II errors.
What statisticians call an alternative hypothesis is simply an hypothesis that contradicts the null hypothesis.

Error[edit]

Working from a null hypothesis two basic forms of error are recognized:
  • Type I errors where the null hypothesis is falsely rejected giving a "false positive".
  • Type II errors where the null hypothesis fails to be rejected and an actual difference between populations is missed giving a "false negative".
Standard deviation refers to the extent to which individual observations in a sample differ from a central value, such as the sample or population mean, while Standard error refers to an estimate of difference between sample mean and population mean.
A statistical error is the amount by which an observation differs from its expected value, a residual is the amount an observation differs from the value the estimator of the expected value assumes on a given sample (also called prediction).
Mean squared error is used for obtaining efficient estimators, a widely used class of estimators. Root mean square error is simply the square root of mean squared error.


A least squares fit: in red the points to be fitted, in blue the fitted line.
Many statistical methods seek to minimize the residual sum of squares, and these are called "methods of least squares" in contrast to Least absolute deviations. The later gives equal weight to small and big errors, while the former gives more weight to large errors. Residual sum of squares is also differentiable, which provides a handy property for doing regression. Least squares applied to linear regression is called ordinary least squares method and least squares applied to nonlinear regression is called non-linear least squares. Also in a linear regression model the non deterministic part of the model is called error term, disturbance or more simply noise. Both linear regression and non-linear regression are addressed in polynomial least squares, which also describes the variance in a prediction of the dependent variable (y axis) as a function of the independent variable (x axis) and the deviations (errors, noise, disturbances) from the estimated (fitted) curve.
Measurement processes that generate statistical data are also subject to error. Many of these errors are classified as random (noise) or systematic (bias), but other important types of errors (e.g., blunder, such as when an analyst reports incorrect units) can also be important. The presence of missing data and/or censoring may result in biased estimates and specific techniques have been developed to address these problems.[17]

Interval estimation[edit]

Main article: Interval estimation


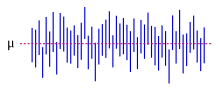
Confidence intervals: the red line is true value for the mean in this example, the blue lines are random confidence intervals for 100 realizations.
Most studies only sample part of a population, so results don't fully represent the whole population. Any estimates obtained from the sample only approximate the population value. Confidence intervals allow statisticians to express how closely the sample estimate matches the true value in the whole population. Often they are expressed as 95% confidence intervals. Formally, a 95% confidence interval for a value is a range where, if the sampling and analysis were repeated under the same conditions (yielding a different dataset), the interval would include the true (population) value in 95% of all possible cases. This does not imply that the probability that the true value is in the confidence interval is 95%. From the frequentist perspective, such a claim does not even make sense, as the true value is not a random variable. Either the true value is or is not within the given interval. However, it is true that, before any data are sampled and given a plan for how to construct the confidence interval, the probability is 95% that the yet-to-be-calculated interval will cover the true value: at this point, the limits of the interval are yet-to-be-observed random variables. One approach that does yield an interval that can be interpreted as having a given probability of containing the true value is to use a credible interval from Bayesian statistics: this approach depends on a different way of interpreting what is meant by "probability", that is as a Bayesian probability.
In principle confidence intervals can be symmetrical or asymmetrical. An interval can be asymmetrical because it works as lower or upper bound for a parameter (left-sided interval or right sided interval), but it can also be asymmetrical because the two sided interval is built violating symmetry around the estimate. Sometimes the bounds for a confidence interval are reached asymptotically and these are used to approximate the true bounds.

Significance[edit]

Main article: Statistical significance
Statistics rarely give a simple Yes/No type answer to the question under analysis. Interpretation often comes down to the level of statistical significance applied to the numbers and often refers to the probability of a value accurately rejecting the null hypothesis (sometimes referred to as the p-value).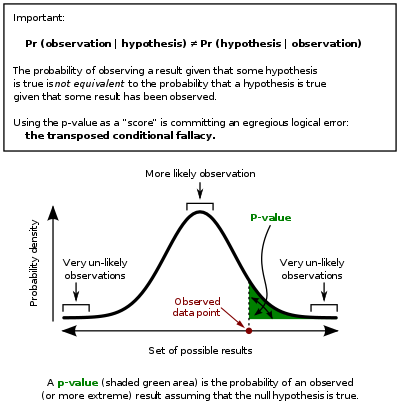


In this graph the black line is probability distribution for the test statistic, the critical region is the set of values to the right of the observed data point (observed value of the test statistic) and the p-value is represented by the green area.
The standard approach[16] is to test a null hypothesis against an alternative hypothesis. A critical region is the set of values of the estimator that leads to refuting the null hypothesis. The probability of type I error is therefore the probability that the estimator belongs to the critical region given that null hypothesis is true (statistical significance) and the probability of type II error is the probability that the estimator doesn't belong to the critical region given that the alternative hypothesis is true. The statistical power of a test is the probability that it correctly rejects the null hypothesis when the null hypothesis is false.
Referring to statistical significance does not necessarily mean that the overall result is significant in real world terms. For example, in a large study of a drug it may be shown that the drug has a statistically significant but very small beneficial effect, such that the drug is unlikely to help the patient noticeably.
While in principle the acceptable level of statistical significance may be subject to debate, the p-value is the smallest significance level that allows the test to reject the null hypothesis. This is logically equivalent to saying that the p-value is the probability, assuming the null hypothesis is true, of observing a result at least as extreme as the test statistic. Therefore the smaller the p-value, the lower the probability of committing type I error.
Some problems are usually associated with this framework (See criticism of hypothesis testing):
  • A difference that is highly statistically significant can still be of no practical significance, but it is possible to properly formulate tests to account for this. One response involves going beyond reporting only the significance level to include the p-value when reporting whether a hypothesis is rejected or accepted. The p-value, however, does not indicate the size or importance of the observed effect and can also seem to exaggerate the importance of minor differences in large studies. A better and increasingly common approach is to report confidence intervals. Although these are produced from the same calculations as those of hypothesis tests or p-values, they describe both the size of the effect and the uncertainty surrounding it.
  • Fallacy of the transposed conditional, aka prosecutor's fallacy: criticisms arise because the hypothesis testing approach forces one hypothesis (the null hypothesis) to be favored, since what is being evaluated is probability of the observed result given the null hypothesis and not probability of the null hypothesis given the observed result. An alternative to this approach is offered by Bayesian inference, although it requires establishing a prior probability.[18]
  • Rejecting the null hypothesis does not automatically prove the alternative hypothesis.
  • As everything in inferential statistics it relies on sample size, and therefore under fat tails p-values may be seriously mis-computed.

Examples[edit]

Some well-known statistical tests and procedures are:

Misuse of statistics[edit]

Main article: Misuse of statistics
Misuse of statistics can produce subtle, but serious errors in description and interpretation—subtle in the sense that even experienced professionals make such errors, and serious in the sense that they can lead to devastating decision errors. For instance, social policy, medical practice, and the reliability of structures like bridges all rely on the proper use of statistics.
Even when statistical techniques are correctly applied, the results can be difficult to interpret for those lacking expertise. The statistical significance of a trend in the data—which measures the extent to which a trend could be caused by random variation in the sample—may or may not agree with an intuitive sense of its significance. The set of basic statistical skills (and skepticism) that people need to deal with information in their everyday lives properly is referred to as statistical literacy.
There is a general perception that statistical knowledge is all-too-frequently intentionally misused by finding ways to interpret only the data that are favorable to the presenter.[19] A mistrust and misunderstanding of statistics is associated with the quotation, "There are three kinds of lies: lies, damned lies, and statistics". Misuse of statistics can be both inadvertent and intentional, and the book How to Lie with Statistics[19] outlines a range of considerations. In an attempt to shed light on the use and misuse of statistics, reviews of statistical techniques used in particular fields are conducted (e.g. Warne, Lazo, Ramos, and Ritter (2012)).[20]
Ways to avoid misuse of statistics include using proper diagrams and avoiding bias.[21] Misuse can occur when conclusions are overgeneralized and claimed to be representative of more than they really are, often by either deliberately or unconsciously overlooking sampling bias.[22] Bar graphs are arguably the easiest diagrams to use and understand, and they can be made either by hand or with simple computer programs.[21] Unfortunately, most people do not look for bias or errors, so they are not noticed. Thus, people may often believe that something is true even if it is not well represented.[22] To make data gathered from statistics believable and accurate, the sample taken must be representative of the whole.[23] According to Huff, "The dependability of a sample can be destroyed by [bias]... allow yourself some degree of skepticism."[24]
To assist in the understanding of statistics Huff proposed a series of questions to be asked in each case:[24]
  • Who says so? (Does he/she have an axe to grind?)
  • How does he/she know? (Does he/she have the resources to know the facts?)
  • What’s missing? (Does he/she give us a complete picture?)
  • Did someone change the subject? (Does he/she offer us the right answer to the wrong problem?)
  • Does it make sense? (Is his/her conclusion logical and consistent with what we already know?)


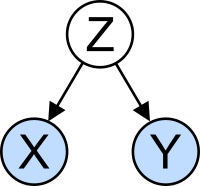
The confounding variable problem: X and Y may be correlated, not because there is causal relationship between them, but because both depend on a third variable Z. Z is called a confounding factor.

Misinterpretation: correlation[edit]

The concept of correlation is particularly noteworthy for the potential confusion it can cause. Statistical analysis of a data set often reveals that two variables (properties) of the population under consideration tend to vary together, as if they were connected. For example, a study of annual income that also looks at age of death might find that poor people tend to have shorter lives than affluent people. The two variables are said to be correlated; however, they may or may not be the cause of one another. The correlation phenomena could be caused by a third, previously unconsidered phenomenon, called a lurking variable or confounding variable. For this reason, there is no way to immediately infer the existence of a causal relationship between the two variables. (See Correlation does not imply causation.)

History of statistical science[edit]



Blaise Pascal, an early pioneer on the mathematics of probability.
Main articles: History of statistics and Founders of statistics
Statistical methods date back at least to the 5th century BC.
Some scholars pinpoint the origin of statistics to 1663, with the publication of Natural and Political Observations upon the Bills of Mortality by John Graunt.[25] Early applications of statistical thinking revolved around the needs of states to base policy on demographic and economic data, hence its stat- etymology. The scope of the discipline of statistics broadened in the early 19th century to include the collection and analysis of data in general. Today, statistics is widely employed in government, business, and natural and social sciences.
Its mathematical foundations were laid in the 17th century with the development of the probability theory by Blaise Pascal and Pierre de Fermat. Mathematical probability theory arose from the study of games of chance, although the concept of probability was already examined in medieval law and by philosophers such as Juan Caramuel.[26] The method of least squares was first described by Adrien-Marie Legendre in 1805.


Karl Pearson, a founder of mathematical statistics.
The modern field of statistics emerged in the late 19th and early 20th century in three stages.[27] The first wave, at the turn of the century, was led by the work of Sir Francis Galton and Karl Pearson, who transformed statistics into a rigorous mathematical discipline used for analysis, not just in science, but in industry and politics as well. Galton's contributions to the field included introducing the concepts of standard deviation, correlation, regression and the application of these methods to the study of the variety of human characteristics – height, weight, eyelash length among others.[28] Pearson developed the Correlation coefficient, defined as a product-moment,[29] the method of moments for the fitting of distributions to samples and the Pearson's system of continuous curves, among many other things.[30] Galton and Pearson founded Biometrika as the first journal of mathematical statistics and biometry, and the latter founded the world's first university statistics department at University College London.[31]


Ronald Fisher coined the term "null hypothesis".
The second wave of the 1910s and 20s was initiated by William Gosset, and reached its culmination in the insights of Sir Ronald Fisher, who wrote the textbooks that were to define the academic discipline in universities around the world. Fisher's most important publications were his 1916 seminal paper The Correlation between Relatives on the Supposition of Mendelian Inheritance and his classic 1925 work Statistical Methods for Research Workers. His paper was the first to use the statistical term, variance. He developed rigorous experimental models and also originated the concepts of sufficiency, ancillary statistics, Fisher's linear discriminator and Fisher information.[32]


Anil Kumar Gain, famous Indian statistician
The final wave, which mainly saw the refinement and expansion of earlier developments, emerged from the collaborative work between Egon Pearson and Jerzy Neyman in the 1930s. They introduced the concepts of "Type II" error, power of a test and confidence intervals. Jerzy Neyman in 1934 showed that stratified random sampling was in general a better method of estimation than purposive (quota) sampling.[33]
Today, statistical methods are applied in all fields that involve decision making, for making accurate inferences from a collated body of data and for making decisions in the face of uncertainty based on statistical methodology. The use of modern computers has expedited large-scale statistical computations, and has also made possible new methods that are impractical to perform manually. Statistics continues to be an area of active research, for example on the problem of how to analyze Big data.[34]

Applications[edit]

Applied statistics, theoretical statistics and mathematical statistics[edit]

"Applied statistics" comprises descriptive statistics and the application of inferential statistics.[35][36] Theoretical statistics concerns both the logical arguments underlying justification of approaches to statistical inference, as well encompassing mathematical statistics. Mathematical statistics includes not only the manipulation of probability distributions necessary for deriving results related to methods of estimation and inference, but also various aspects of computational statistics and the design of experiments.

Machine learning and data mining[edit]

There are two applications for machine learning and data mining: data management and data analysis. Statistics tools are necessary for the data analysis.

Statistics in society[edit]

Statistics is applicable to a wide variety of academic disciplines, including natural and social sciences, government, and business. Statistical consultants can help organizations and companies that don't have in-house expertise relevant to their particular questions.

Statistical computing[edit]



gretl, an example of an open source statistical package
Main article: Computational statistics
The rapid and sustained increases in computing power starting from the second half of the 20th century have had a substantial impact on the practice of statistical science. Early statistical models were almost always from the class of linear models, but powerful computers, coupled with suitable numerical algorithms, caused an increased interest in nonlinear models (such as neural networks) as well as the creation of new types, such as generalized linear models and multilevel models.
Increased computing power has also led to the growing popularity of computationally intensive methods based on resampling, such as permutation tests and the bootstrap, while techniques such as Gibbs sampling have made use of Bayesian models more feasible. The computer revolution has implications for the future of statistics with new emphasis on "experimental" and "empirical" statistics. A large number of both general and special purpose statistical software are now available.

Statistics applied to mathematics or the arts[edit]

Traditionally, statistics was concerned with drawing inferences using a semi-standardized methodology that was "required learning" in most sciences. This has changed with use of statistics in non-inferential contexts. What was once considered a dry subject, taken in many fields as a degree-requirement, is now viewed enthusiastically.[according to whom?] Initially derided by some mathematical purists, it is now considered essential methodology in certain areas.
  • In number theory, scatter plots of data generated by a distribution function may be transformed with familiar tools used in statistics to reveal underlying patterns, which may then lead to hypotheses.
  • Methods of statistics including predictive methods in forecasting are combined with chaos theory and fractal geometry to create video works that are considered to have great beauty.[citation needed]
  • The process art of Jackson Pollock relied on artistic experiments whereby underlying distributions in nature were artistically revealed.[citation needed] With the advent of computers, statistical methods were applied to formalize such distribution-driven natural processes to make and analyze moving video art.[citation needed]
  • Methods of statistics may be used predicatively in performance art, as in a card trick based on a Markov process that only works some of the time, the occasion of which can be predicted using statistical methodology.
  • Statistics can be used to predicatively create art, as in the statistical or stochastic music invented by Iannis Xenakis, where the music is performance-specific. Though this type of artistry does not always come out as expected, it does behave in ways that are predictable and tunable using statistics.

Specialized disciplines[edit]

Main article: List of fields of application of statistics
Statistical techniques are used in a wide range of types of scientific and social research, including: biostatistics, computational biology, computational sociology, network biology, social science, sociology and social research. Some fields of inquiry use applied statistics so extensively that they have specialized terminology. These disciplines include:
In addition, there are particular types of statistical analysis that have also developed their own specialised terminology and methodology:
Statistics form a key basis tool in business and manufacturing as well. It is used to understand measurement systems variability, control processes (as in statistical process control or SPC), for summarizing data, and to make data-driven decisions. In these roles, it is a key tool, and perhaps the only reliable tool.

See also[edit]

Find more about
Statistics
at Wikipedia's sister projects
Search WiktionaryDefinitions from Wiktionary
Search CommonsMedia from Commons
Search WikinewsNews stories from Wikinews
Search WikiquoteQuotations from Wikiquote
Search WikisourceSource texts from Wikisource
Search WikibooksTextbooks from Wikibooks
Search WikiversityLearning resources from Wikiversity
Library resources about
Statistics
Main article: Outline of statistics
Foundations and major areas of statistics

References[edit]

  1. ^ Jump up to: a b Dodge, Y. (2006) The Oxford Dictionary of Statistical Terms, OUP. ISBN 0-19-920613-9
  2. Jump up ^ Lund Research Ltd. "Descriptive and Inferential Statistics". statistics.laerd.com. Retrieved 2014-03-23. 
  3. Jump up ^ Moses, Lincoln E. (1986) Think and Explain with Statistics, Addison-Wesley, ISBN 978-0-201-15619-5 . pp. 1–3
  4. Jump up ^ Hays, William Lee, (1973) Statistics for the Social Sciences, Holt, Rinehart and Winston, p.xii, ISBN 978-0-03-077945-9
  5. Jump up ^ Moore, David (1992). "Teaching Statistics as a Respectable Subject". In F. Gordon and S. Gordon. Statistics for the Twenty-First Century. Washington, DC: The Mathematical Association of America. pp. 14–25. ISBN 978-0-88385-078-7. 
  6. Jump up ^ Chance, Beth L.; Rossman, Allan J. (2005). "Preface". Investigating Statistical Concepts, Applications, and Methods (PDF). Duxbury Press. ISBN 978-0-495-05064-3. 
  7. Jump up ^ Lakshmikantham,, ed. by D. Kannan,... V. (2002). Handbook of stochastic analysis and applications. New York: M. Dekker. ISBN 0824706609. 
  8. Jump up ^ Schervish, Mark J. (1995). Theory of statistics (Corr. 2nd print. ed.). New York: Springer. ISBN 0387945466. 
  9. Jump up ^ Freedman, D.A. (2005) Statistical Models: Theory and Practice, Cambridge University Press. ISBN 978-0-521-67105-7
  10. Jump up ^ McCarney R, Warner J, Iliffe S, van Haselen R, Griffin M, Fisher P (2007). "The Hawthorne Effect: a randomised, controlled trial". BMC Med Res Methodol 7 (1): 30. doi:10.1186/1471-2288-7-30. PMC 1936999. PMID 17608932. 
  11. Jump up ^ Mosteller, F., & Tukey, J. W. (1977). Data analysis and regression. Boston: Addison-Wesley.
  12. Jump up ^ Nelder, J. A. (1990). The knowledge needed to computerise the analysis and interpretation of statistical information. In Expert systems and artificial intelligence: the need for information about data. Library Association Report, London, March, 23–27.
  13. Jump up ^ Chrisman, Nicholas R (1998). "Rethinking Levels of Measurement for Cartography". Cartography and Geographic Information Science 25 (4): 231–242. doi:10.1559/152304098782383043. 
  14. Jump up ^ van den Berg, G. (1991). Choosing an analysis method. Leiden: DSWO Press
  15. Jump up ^ Hand, D. J. (2004). Measurement theory and practice: The world through quantification. London, UK: Arnold.
  16. ^ Jump up to: a b Piazza Elio, Probabilità e Statistica, Esculapio 2007
  17. Jump up ^ Rubin, Donald B.; Little, Roderick J. A.,Statistical analysis with missing data, New York: Wiley 2002
  18. Jump up ^ Ioannidis, J. P. A. (2005). "Why Most Published Research Findings Are False". PLoS Medicine 2 (8): e124. doi:10.1371/journal.pmed.0020124. PMC 1182327. PMID 16060722.  edit
  19. ^ Jump up to: a b Huff, Darrell (1954) How to Lie with Statistics, WW Norton & Company, Inc. New York, NY. ISBN 0-393-31072-8
  20. Jump up ^ Warne, R. Lazo; Ramos, T.; Ritter, N. (2012). "Statistical Methods Used in Gifted Education Journals, 2006–2010". Gifted Child Quarterly 56 (3): 134–149. doi:10.1177/0016986212444122. 
  21. ^ Jump up to: a b Drennan, Robert D. (2008). "Statistics in archaeology". In Pearsall, Deborah M. Encyclopedia of Archaeology. Elsevier Inc. pp. 2093–2100. ISBN 978-0-12-373962-9. 
  22. ^ Jump up to: a b Cohen, Jerome B. (December 1938). "Misuse of Statistics". Journal of the American Statistical Association (JSTOR) 33 (204): 657–674. doi:10.1080/01621459.1938.10502344. 
  23. Jump up ^ Freund, J. E. (1988). "Modern Elementary Statistics". Credo Reference. 
  24. ^ Jump up to: a b Huff, Darrell; Irving Geis (1954). How to Lie with Statistics. New York: Norton. The dependability of a sample can be destroyed by [bias]... allow yourself some degree of skepticism. 
  25. Jump up ^ Willcox, Walter (1938) "The Founder of Statistics". Review of the International Statistical Institute 5(4):321–328. JSTOR 1400906
  26. Jump up ^ J. Franklin, The Science of Conjecture: Evidence and Probability before Pascal,Johns Hopkins Univ Pr 2002
  27. Jump up ^ Helen Mary Walker (1975). Studies in the history of statistical method. Arno Press. 
  28. Jump up ^ Galton, F (1877). "Typical laws of heredity". Nature 15: 492–553. doi:10.1038/015492a0. 
  29. Jump up ^ Stigler, S. M. (1989). "Francis Galton's Account of the Invention of Correlation". Statistical Science 4 (2): 73–79. doi:10.1214/ss/1177012580. 
  30. Jump up ^ Pearson, K. (1900). "On the Criterion that a given System of Deviations from the Probable in the Case of a Correlated System of Variables is such that it can be reasonably supposed to have arisen from Random Sampling". Philosophical Magazine Series 5 50 (302): 157–175. doi:10.1080/14786440009463897. 
  31. Jump up ^ "Karl Pearson (1857–1936)". Department of Statistical Science – University College London. 
  32. Jump up ^ Agresti, Alan; David B. Hichcock (2005). "Bayesian Inference for Categorical Data Analysis" (PDF). Statistical Methods & Applications 14 (14): 298. doi:10.1007/s10260-005-0121-y. 
  33. Jump up ^ Neyman, J (1934). "On the two different aspects of the representative method: The method of stratified sampling and the method of purposive selection". Journal of the Royal Statistical Society 97 (4): 557–625. JSTOR 2342192. 
  34. Jump up ^ "Science in a Complex World - Big Data: Opportunity or Threat?". Santa Fe Institute. 
  35. Jump up ^ Nikoletseas, M. M. (2014) "Statistics: Concepts and Examples." ISBN 978-1500815684
  36. Jump up ^ Anderson, D.R.; Sweeney, D.J.; Williams, T.A. (1994) Introduction to Statistics: Concepts and Applications, pp. 5–9. West Group. ISBN 978-0-314-03309-3
Authority control
Retrieved from "http://en.wikipedia.org/w/index.php?title=Statistics&oldid=665187201"
at
Labels: , ,

No comments:

Post a Comment

Subscribe to: Post Comments (Atom)

Welcome to Precision Universal Debate

  IMPORTANT Though the title of this p2p entry is the Universal Debating Project (at present) it has now been re-named the Precision Univers...

  • Consensus decion-making
    Blogger Ref Universal Debating Project Consensus decision-making is a group decision-making process in which group members develop, and ...
  • Reliability of Wikipedia
      From Wikipedia, the free encyclopedia/Blogger Ref   http://www.p2pfoundation.net/Universal_Debating_Project     (Redirected from W...
  • Committee
    From Wikipedia, the free encyclopedia    Blogger Ref Universal Debating Project Jump to: navigation , search For othe...