Friday, 25 August 2017

A Decision Tree

Blogger ref Universal Debating Project




A decision tree is a decision support tool that uses a tree-like graph or model of decisions and their possible consequences, including chance event outcomes, resource costs, and utility. It is one way to display an algorithm.
Decision trees are commonly used in operations research, specifically in decision analysis, to help identify a strategy most likely to reach a goal, but are also a popular tool in machine learning.


Overview[edit]

A decision tree is a flowchart-like structure in which each internal node represents a "test" on an attribute (e.g. whether a coin flip comes up heads or tails), each branch represents the outcome of the test, and each leaf node represents a class label (decision taken after computing all attributes). The paths from root to leaf represent classification rules.
In decision analysis, a decision tree and the closely related influence diagram are used as a visual and analytical decision support tool, where the expected values (or expected utility) of competing alternatives are calculated.
A decision tree consists of three types of nodes:[1]
  1. Decision nodes – typically represented by squares
  2. Chance nodes – typically represented by circles
  3. End nodes – typically represented by triangles
Decision trees are commonly used in operations research and operations management. If, in practice, decisions have to be taken online with no recall under incomplete knowledge, a decision tree should be paralleled by a probability model as a best choice model or online selection model algorithm. Another use of decision trees is as a descriptive means for calculating conditional probabilities.
Decision trees, influence diagrams, utility functions, and other decision analysis tools and methods are taught to undergraduate students in schools of business, health economics, and public health, and are examples of operations research or management science methods.

Decision tree building blocks[edit]

Decision tree elements[edit]

Decision-Tree-Elements.png
Drawn from left to right, a decision tree has only burst nodes (splitting paths) but no sink nodes (converging paths). Therefore, used manually, they can grow very big and are then often hard to draw fully by hand. Traditionally, decision trees have been created manually — as the aside example shows — although increasingly, specialized software is employed.

Decision rules[edit]

The decision tree can be linearized into decision rules,[2] where the outcome is the contents of the leaf node, and the conditions along the path form a conjunction in the if clause. In general, the rules have the form:
if condition1 and condition2 and condition3 then outcome.
Decision rules can be generated by constructing association rules with the target variable on the right. They can also denote temporal or causal relations.[3]

Decision tree using flowchart symbols[edit]

Commonly a decision tree is drawn using flowchart symbols as it is easier for many to read and understand.
DecisionCalcs.jpg

Analysis example[edit]

Analysis can take into account the decision maker's (e.g., the company's) preference or utility function, for example:
RiskPrefSensitivity2Threshold.png
The basic interpretation in this situation is that the company prefers B's risk and payoffs under realistic risk preference coefficients (greater than $400K—in that range of risk aversion, the company would need to model a third strategy, "Neither A nor B").

Influence diagram[edit]

Much of the information in a decision tree can be represented more compactly as an influence diagram, focusing attention on the issues and relationships between events.

The rectangle on the left represents a decision, the ovals represent actions, and the diamond represents results.

Association rule induction[edit]

Decision trees can also be seen as generative models of induction rules from empirical data. An optimal decision tree is then defined as a tree that accounts for most of the data, while minimizing the number of levels (or "questions").[4] Several algorithms to generate such optimal trees have been devised, such as ID3/4/5,[5] CLS, ASSISTANT, and CART.

Advantages and disadvantages[edit]

Among decision support tools, decision trees (and influence diagrams) have several advantages. Decision trees:
  • Are simple to understand and interpret. People are able to understand decision tree models after a brief explanation.
  • Have value even with little hard data. Important insights can be generated based on experts describing a situation (its alternatives, probabilities, and costs) and their preferences for outcomes.
  • Allow the addition of new possible scenarios.
  • Help determine worst, best and expected values for different scenarios.
  • Use a white box model. If a given result is provided by a model.
  • Can be combined with other decision techniques.
Disadvantages of decision trees:
  • For data including categorical variables with different number of levels, information gain in decision trees is biased in favor of those attributes with more levels.[6]
  • Calculations can get very complex, particularly if many values are uncertain and/or if many outcomes are linked.

See also[edit]

References[edit]

  1. Jump up ^ Kamiński, B.; Jakubczyk, M.; Szufel, P. (2017). "A framework for sensitivity analysis of decision trees". Central European Journal of Operations Research. doi:10.1007/s10100-017-0479-6. 
  2. Jump up ^ Quinlan, J. R. (1987). "Simplifying decision trees". International Journal of Man-Machine Studies. 27 (3): 221. doi:10.1016/S0020-7373(87)80053-6. 
  3. Jump up ^ K. Karimi and H.J. Hamilton (2011), "Generation and Interpretation of Temporal Decision Rules", International Journal of Computer Information Systems and Industrial Management Applications, Volume 3
  4. Jump up ^ R. Quinlan, "Learning efficient classification procedures", Machine Learning: an artificial intelligence approach, Michalski, Carbonell & Mitchell (eds.), Morgan Kaufmann, 1983, p. 463-482. doi:10.1007/978-3-662-12405-5_15
  5. Jump up ^ Utgoff, P. E. (1989). Incremental induction of decision trees. Machine learning, 4(2), 161-186. doi:10.1023/A:1022699900025
  6. Jump up ^ Deng,H.; Runger, G.; Tuv, E. (2011). Bias of importance measures for multi-valued attributes and solutions. Proceedings of the 21st International Conference on Artificial Neural Networks (ICANN). 

Further reading[edit]

External links[edit]


Retrieved from "https://en.wikipedia.org/w/index.php?title=Decision_tree&oldid=794707745"
at No comments:
Labels: , ,

Argument map

From Wikipedia, the free encyclopedia/Blogger ref Universal Debating Project
Jump to: navigation, search


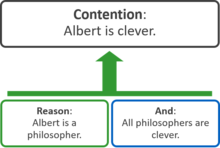
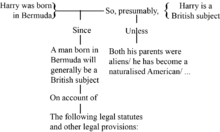
A schematic argument map showing a contention (or conclusion), supporting arguments and objections, and an inference objection.
Part of "School of Athens" by Raphael (Raffaelo Sanzio, 1483-1520)
Information mapping
Topics & fields
Node–link approaches
See also
In informal logic and philosophy, an argument map or argument diagram is a visual representation of the structure of an argument. An argument map typically includes the key components of the argument, traditionally called the conclusion and the premises, also called contention and reasons.[1] Argument maps can also show co-premises, objections, counterarguments, rebuttals, and lemmas. There are different styles of argument map but they are often functionally equivalent and represent an argument's individual claims and the relationships between them.
Argument maps are commonly used in the context of teaching and applying critical thinking.[2] The purpose of mapping is to uncover the logical structure of arguments, identify unstated assumptions, evaluate the support an argument offers for a conclusion, and aid understanding of debates. Argument maps are often designed to support deliberation of issues, ideas and arguments in wicked problems.[3]
An argument map is not to be confused with a concept map or a mind map, two other kinds of node–link diagram which have different constraints on nodes and links.[4]


Key features of an argument map[edit]

A number of different kinds of argument map have been proposed but the most common, which Chris Reed and Glenn Rowe called the standard diagram,[5] consists of a tree structure with each of the reasons leading to the conclusion. There is no consensus as to whether the conclusion should be at the top of the tree with the reasons leading up to it or whether it should be at the bottom with the reasons leading down to it.[5] Another variation diagrams an argument from left to right.[6]
According to Doug Walton and colleagues, an argument map has two basic components: "One component is a set of circled numbers arrayed as points. Each number represents a proposition (premise or conclusion) in the argument being diagrammed. The other component is a set of lines or arrows joining the points. Each line (arrow) represents an inference. The whole network of points and lines represents a kind of overview of the reasoning in the given argument..."[7] With the introduction of software for producing argument maps, it has become common for argument maps to consist of boxes containing the actual propositions rather than numbers referencing those propositions.
There is disagreement on the terminology to be used when describing argument maps,[8] but the standard diagram contains the following structures:
Dependent premises or co-premises, where at least one of the joined premises requires another premise before it can give support to the conclusion: An argument with this structure has been called a linked argument.[9]


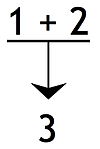
Statements 1 and 2 are dependent premises or co-premises
Independent premises, where the premise can support the conclusion on its own: Although independent premises may jointly make the conclusion more convincing, this is to be distinguished from situations where a premise gives no support unless it is joined to another premise. Where several premises or groups of premises lead to a final conclusion the argument might be described as convergent. This is distinguished from a divergent argument where a single premise might be used to support two separate conclusions.[10]


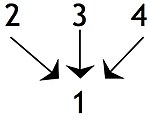
Statements 2, 3, 4 are independent premises
Intermediate conclusions or sub-conclusions, where a claim is supported by another claim that is used in turn to support some further claim, i.e. the final conclusion or another intermediate conclusion: In the following diagram, statement 4 is an intermediate conclusion in that it is a conclusion in relation to statement 5 but is a premise in relation to the final conclusion, i.e. statement 1. An argument with this structure is sometimes called a complex argument. If there is a single chain of claims containing at least one intermediate conclusion, the argument is sometimes described as a serial argument or a chain argument.[11]


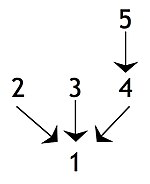
Statement 4 is an intermediate conclusion or sub-conclusion
Each of these structures can be represented by the equivalent "box and line" approach to argument maps. In the following diagram, the contention is shown at the top, and the boxes linked to it represent supporting reasons, which comprise one or more premises. The green arrow indicates that the two reasons support the contention:


A box and line diagram
Argument maps can also represent counterarguments. In the following diagram, the two objections weaken the contention, while the reasons support the premise of the objection:


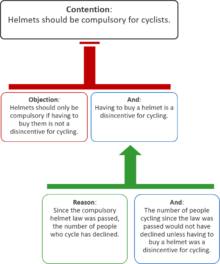
A sample argument using objections

Representing an argument as an argument map[edit]

A written text can be transformed into an argument map by following a sequence of steps. Monroe Beardsley's 1950 book Practical Logic recommended the following procedure:[12]
  1. Separate statements by brackets and number them.
  2. Put circles around the logical indicators.
  3. Supply, in parenthesis, any logical indicators that are left out.
  4. Set out the statements in a diagram in which arrows show the relationships between statements.


A diagram of the example from Beardsley's Practical Logic
Beardsley gave the first example of a text being analysed in this way:
Though ① [people who talk about the "social significance" of the arts don’t like to admit it], ② [music and painting are bound to suffer when they are turned into mere vehicles for propaganda]. For ③ [propaganda appeals to the crudest and most vulgar feelings]: (for) ④ [look at the academic monstrosities produced by the official Nazi painters]. What is more important, ⑤ [art must be an end in itself for the artist], because ⑥ [the artist can do the best work only in an atmosphere of complete freedom].
Beardsley said that the conclusion in this example is statement ②. Statement ④ needs to be rewritten as a declarative sentence, e.g. "Academic monstrosities [were] produced by the official Nazi painters." Statement ① points out that the conclusion isn't accepted by everyone, but statement ① is omitted from the diagram because it doesn't support the conclusion. Beardsley said that the logical relation between statement ③ and statement ④ is unclear, but he proposed to diagram statement ④ as supporting statement ③.


A box and line diagram of Beardsley's example, produced using Harrell's procedure
More recently, philosophy professor Maralee Harrell recommended the following procedure:[13]
  1. Identify all the claims being made by the author.
  2. Rewrite them as independent statements, eliminating non-essential words.
  3. Identify which statements are premises, sub-conclusions, and the main conclusion.
  4. Provide missing, implied conclusions and implied premises. (This is optional depending on the purpose of the argument map.)
  5. Put the statements into boxes and draw a line between any boxes that are linked.
  6. Indicate support from premise(s) to (sub)conclusion with arrows.
Argument maps are useful not only for representing and analyzing existing writings, but also for thinking through issues as part of a problem-structuring process or writing process. The use of such argument analysis for thinking through issues has been called "reflective argumentation".[14]
An argument map, unlike a decision tree, does not tell how to make a decision, but the process of choosing a coherent position (or reflective equilibrium) based on the structure of an argument map can be represented as a decision tree.[15]

History[edit]

The philosophical origins and tradition of argument mapping[edit]



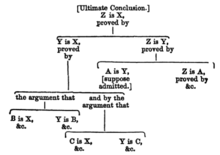
From Whately's Elements of Logic p467, 1852 edition
In the Elements of Logic, which was published in 1826 and issued in many subsequent editions,[16] Archbishop Richard Whately gave probably the first form of an argument map, introducing it with the suggestion that "many students probably will find it a very clear and convenient mode of exhibiting the logical analysis of the course of argument, to draw it out in the form of a Tree, or Logical Division".
However, the technique did not become widely used, possibly because for complex arguments, it involved much writing and rewriting of the premises.


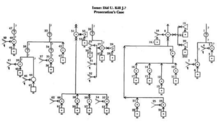
Wigmore evidence chart, from 1905
Legal philosopher and theorist John Henry Wigmore produced maps of legal arguments using numbered premises in the early 20th century,[17] based in part on the ideas of 19th century philosopher Henry Sidgwick who used lines to indicate relations between terms.[18]

Anglophone argument diagramming in the 20th century[edit]

Dealing with the failure of formal reduction of informal argumentation, English speaking argumentation theory developed diagrammatic approaches to informal reasoning over a period of fifty years.
Monroe Beardsley proposed a form of argument diagram in 1950.[12] His method of marking up an argument and representing its components with linked numbers became a standard and is still widely used. He also introduced terminology that is still current describing convergent, divergent and serial arguments.


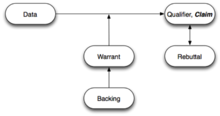
A Toulmin argument diagram, redrawn from his 1959 Uses of Argument


A generalised Toulmin diagram
Stephen Toulmin, in his groundbreaking and influential 1958 book The Uses of Argument,[19] identified several elements to an argument which have been generalized. The Toulmin diagram is widely used in educational critical teaching.[20][21] Whilst Toulmin eventually had a significant impact on the development of informal logic he had little initial impact and the Beardsley approach to diagramming arguments along with its later developments became the standard approach in this field. Toulmin introduced something that was missing from Beardsley's approach. In Beardsley, "arrows link reasons and conclusions (but) no support is given to the implication itself between them. There is no theory, in other words, of inference distinguished from logical deduction, the passage is always deemed not controversial and not subject to support and evaluation".[22] Toulmin introduced the concept of warrant which "can be considered as representing the reasons behind the inference, the backing that authorizes the link".[23]
Beardsley's approach was refined by Stephen N. Thomas, whose 1973 book Practical Reasoning In Natural Language[24] introduced the term linked to describe arguments where the premises necessarily worked together to support the conclusion.[25] However, the actual distinction between dependent and independent premises had been made prior to this.[25] The introduction of the linked structure made it possible for argument maps to represent missing or "hidden" premises. In addition, Thomas suggested showing reasons both for and against a conclusion with the reasons against being represented by dotted arrows. Thomas introduced the term argument diagram and defined basic reasons as those that were not supported by any others in the argument and the final conclusion as that which was not used to support any further conclusion.


Scriven's argument diagram. The explicit premise 1 is conjoined with additional unstated premises a and b to imply 2.
Michael Scriven further developed the Beardsley-Thomas approach in his 1976 book Reasoning.[26] Whereas Beardsley had said "At first, write out the statements...after a little practice, refer to the statements by number alone"[27] Scriven advocated clarifying the meaning of the statements, listing them and then using a tree diagram with numbers to display the structure. Missing premises (unstated assumptions) were to be included and indicated with an alphabetical letter instead of a number to mark them off from the explicit statements. Scriven introduced counterarguments in his diagrams, which Toulmin had defined as rebuttal.[28] This also enabled the diagramming of "balance of consideration" arguments.[29]
In the 1990s, Tim van Gelder and colleagues developed a series of computer software applications that permitted the premises to be fully stated and edited in the diagram, rather than in a legend.[30] Van Gelder's first program, Reason!Able, was superseded by two subsequent programs, bCisive and Rationale.[31]
Throughout the 1990s and 2000s, many other software applications were developed for argument visualization. By 2013, more than 60 such software systems existed.[32] One of the differences between these software systems is whether collaboration is supported.[33] Single-user argumentation systems include Convince Me, iLogos, LARGO, Athena, Araucaria, and Carneades; small group argumentation systems include Digalo, QuestMap, Compendium, Belvedere, and AcademicTalk; community argumentation systems include Debategraph and Collaboratorium.[33] For more software examples, see: § External links.
In 1998 a series of large-scale argument maps released by Robert E. Horn stimulated widespread interest in argument mapping.[34]

Applications[edit]

Argument maps have been applied in many areas, but foremost in educational, academic and business settings, including design rationale.[35] Argument maps are also used in forensic science,[36] law, and artificial intelligence.[37] It has also been proposed that argument mapping has a great potential to improve how we understand and execute democracy, in reference to the ongoing evolution of e-democracy.[38]

Difficulties with the philosophical tradition[edit]

It has traditionally been hard to separate teaching critical thinking from the philosophical tradition of teaching logic and method, and most critical thinking textbooks have been written by philosophers. Informal logic textbooks are replete with philosophical examples, but it is unclear whether the approach in such textbooks transfers to non-philosophy students.[20] There appears to be little statistical effect after such classes. Argument mapping, however, has a measurable effect according to many studies.[39] For example, instruction in argument mapping has been shown to improve the critical thinking skills of business students.[40]

Evidence that argument mapping improves critical thinking ability[edit]

There is empirical evidence that the skills developed in argument-mapping-based critical thinking courses substantially transfer to critical thinking done without argument maps. Alvarez's meta-analysis found that such critical thinking courses produced gains of around 0.70 SD, about twice as much as standard critical-thinking courses.[41] The tests used in the reviewed studies were standard critical-thinking tests.

How argument mapping helps with critical thinking[edit]

The use of argument mapping has occurred within a number of disciplines, such as philosophy, management reporting, military and intelligence analysis, and public debates.[35]
  • Logical structure: Argument maps display an argument's logical structure more clearly than does the standard linear way of presenting arguments.
  • Critical thinking concepts: In learning to argument map, students master such key critical thinking concepts as "reason", "objection", "premise", "conclusion", "inference", "rebuttal", "unstated assumption", "co-premise", "strength of evidence", "logical structure", "independent evidence", etc. Mastering such concepts is not just a matter of memorizing their definitions or even being able to apply them correctly; it is also understanding why the distinctions these words mark are important and using that understanding to guide one's reasoning.
  • Visualization: Humans are highly visual and argument mapping may provide students with a basic set of visual schemas with which to understand argument structures.
  • More careful reading and listening: Learning to argument map teaches people to read and listen more carefully, and highlights for them the key questions "What is the logical structure of this argument?" and "How does this sentence fit into the larger structure?" In-depth cognitive processing is thus more likely.
  • More careful writing and speaking: Argument mapping helps people to state their reasoning and evidence more precisely, because the reasoning and evidence must fit explicitly into the map's logical structure.
  • Literal and intended meaning: Often, many statements in an argument do not precisely assert what the author meant. Learning to argument map enhances the complex skill of distinguishing literal from intended meaning.
  • Externalization: Writing something down and reviewing what one has written often helps reveal gaps and clarify one's thinking. Because the logical structure of argument maps is clearer than that of linear prose, the benefits of mapping will exceed those of ordinary writing.
  • Anticipating replies: Important to critical thinking is anticipating objections and considering the plausibility of different rebuttals. Mapping develops this anticipation skill, and so improves analysis.

Standards[edit]

Argument Interchange Format[edit]

The Argument Interchange Format, AIF, is an international effort to develop a representational mechanism for exchanging argument resources between research groups, tools, and domains using a semantically rich language.[42] AIF-RDF is the extended ontology represented in the Resource Description Framework Schema (RDFS) semantic language. Though AIF is still something of a moving target, it is settling down.[43]

Legal Knowledge Interchange Format[edit]

The Legal Knowledge Interchange Format (LKIF),[44] developed in the European ESTRELLA project,[45] is an XML schema for rules and arguments, designed with the goal of becoming a standard for representing and interchanging policy, legislation and cases, including their justificatory arguments, in the legal domain. LKIF builds on and uses the Web Ontology Language (OWL) for representing concepts and includes a reusable basic ontology of legal concepts.

See also[edit]

Notes[edit]

  1. Jump up ^ Freeman 1991, pp. 49–90
  2. Jump up ^ For example: Davies 2012; Facione 2013, p. 86; Fisher 2004; Kelley 2014, p. 73; Kunsch, Schnarr & van Tyle 2014; Walton 2013, p. 10
  3. Jump up ^ For example: Culmsee & Awati 2013; Hoffmann & Borenstein 2013; Metcalfe & Sastrowardoyo 2013; Ricky Ohl, "Computer supported argument visualisation: modelling in consultative democracy around wicked problems", in Okada, Buckingham Shum & Sherborne 2014, pp. 361–380
  4. Jump up ^ For example: Davies 2010; Hunter 2008; Okada, Buckingham Shum & Sherborne 2014, pp. vii–x, 4
  5. ^ Jump up to: a b Reed & Rowe 2007, p. 64
  6. Jump up ^ For example: Walton 2013, pp. 18–20
  7. Jump up ^ Reed, Walton & Macagno 2007, p. 2
  8. Jump up ^ Freeman 1991, pp. 49–90; Reed & Rowe 2007
  9. Jump up ^ Harrell 2010, p. 19
  10. Jump up ^ Freeman 1991, pp. 91–110; Harrell 2010, p. 20
  11. Jump up ^ Beardsley 1950, pp. 18–19; Reed, Walton & Macagno 2007, pp. 3–8; Harrell 2010, pp. 19–21
  12. ^ Jump up to: a b Beardsley 1950
  13. Jump up ^ Harrell 2010, p. 28
  14. Jump up ^ For example: Hoffmann & Borenstein 2013; Hoffmann 2016
  15. Jump up ^ See section 4.2, "Argument maps as reasoning tools", in Brun & Betz 2016
  16. Jump up ^ Whately 1834 (first published 1826)
  17. Jump up ^ Wigmore 1913
  18. Jump up ^ Goodwin 2000
  19. Jump up ^ Toulmin 2003 (first published 1958)
  20. ^ Jump up to: a b Simon, Erduran & Osborne 2006
  21. Jump up ^ Böttcher & Meisert 2011; Macagno & Konstantinidou 2013
  22. Jump up ^ Reed, Walton & Macagno 2007, p. 8
  23. Jump up ^ Reed, Walton & Macagno 2007, p. 9
  24. Jump up ^ Thomas 1997 (first published 1973)
  25. ^ Jump up to: a b Snoeck Henkemans 2000, p. 453
  26. Jump up ^ Scriven 1976
  27. Jump up ^ Beardsley 1950, p. 21
  28. Jump up ^ Reed, Walton & Macagno 2007, pp. 10–11
  29. Jump up ^ van Eemeren et al. 1996, p. 175
  30. Jump up ^ van Gelder 2007
  31. Jump up ^ Berg et al. 2009
  32. Jump up ^ Walton 2013, p. 11
  33. ^ Jump up to: a b Scheuer et al. 2010
  34. Jump up ^ Holmes 1999; Horn 1998 and Robert E. Horn, "Infrastructure for navigating interdisciplinary debates: critical decisions for representing argumentation", in Kirschner, Buckingham Shum & Carr 2003, pp. 165–184
  35. ^ Jump up to: a b Kirschner, Buckingham Shum & Carr 2003; Okada, Buckingham Shum & Sherborne 2014
  36. Jump up ^ For example: Bex 2011
  37. Jump up ^ For example: Verheij 2005; Reed, Walton & Macagno 2007; Walton 2013
  38. Jump up ^ Hilbert 2009
  39. Jump up ^ Twardy 2004; Álvarez Ortiz 2007; Harrell 2008; Yanna Rider and Neil Thomason, "Cognitive and pedagogical benefits of argument mapping: LAMP guides the way to better thinking", in Okada, Buckingham Shum & Sherborne 2014, pp. 113–134; Dwyer 2011; Davies 2012
  40. Jump up ^ Carrington et al. 2011; Kunsch, Schnarr & van Tyle 2014
  41. Jump up ^ Álvarez Ortiz 2007, pp. 69–70 et seq
  42. Jump up ^ See the AIF original draft description (2006) and the full AIF-RDF ontology specifications in RDFS format.
  43. Jump up ^ Bex et al. 2013
  44. Jump up ^ Boer, Winkels & Vitali 2008
  45. Jump up ^ "Estrella project website". estrellaproject.org. Archived from the original on 2016-02-12. Retrieved 2016-02-24. 

References[edit]

Further reading[edit]

External links[edit]

Argument mapping software[edit]

Online, collaborative software[edit]

Retrieved from "https://en.wikipedia.org/w/index.php?title=Argument_map&oldid=796999915"
at No comments:
Labels: , , ,
Subscribe to: Posts (Atom)

Welcome to Precision Universal Debate

  IMPORTANT Though the title of this p2p entry is the Universal Debating Project (at present) it has now been re-named the Precision Univers...

  • Committee
    From Wikipedia, the free encyclopedia    Blogger Ref Universal Debating Project Jump to: navigation , search For othe...
  • Consensus decion-making
    Blogger Ref Universal Debating Project Consensus decision-making is a group decision-making process in which group members develop, and ...
  • Reliability of Wikipedia
      From Wikipedia, the free encyclopedia/Blogger Ref   http://www.p2pfoundation.net/Universal_Debating_Project     (Redirected from W...