The following could have some serious "indirect" bearing on the Universal Debating Project, and hence, its inclusion here. See http://www.p2pfoundation.net/Universal_Debating_Project
Also, please note the following link on this self same subject.
Melvyn Bragg and guests discuss the problem of P versus NP, which has a bearing on online security. There is a $1,000,000 prize on offer from the Clay Mathematical Institute for the first person to come up with a complete solution. At its heart is the question "are there problems for which the answers can be checked by computers, but not found in a reasonable time?" If the answer to that is yes, then P does not equal NP. However, if all answers can be found easily as well as checked, if only we knew how, then P equals NP. The area has intrigued mathematicians and computer scientists since Alan Turing, in 1936, found that it's impossible to decide in general whether an algorithm will run forever on some problems. Resting on P versus NP is the security of all online transactions which are currently encrypted: if it transpires that P=NP, if answers could be found as easily as checked, computers could crack passwords in moments.
With
Colva Roney-Dougal
Reader in Pure Mathematics at the University of St Andrews
Reader in Pure Mathematics at the University of St Andrews
Timothy Gowers
Royal Society Research Professor in Mathematics at the University of Cambridge
Royal Society Research Professor in Mathematics at the University of Cambridge
And
Leslie Ann Goldberg
Professor of Computer Science and Fellow of St Edmund Hall, University of Oxford
Professor of Computer Science and Fellow of St Edmund Hall, University of Oxford
Producer: Simon Tillotson.
LINKS AND FURTHER READING
Colva Roney-Dougal at the University of St Andrews
Timothy Gowers at the University of Cambridge
Leslie Ann Goldberg at the University of Oxford
P versus NP problem - Wikipedia
P vs. NP for Dummies
Gödel’s Lost Letter and P=NP
MacTutor History of Mathematics archive
READING LIST:
Scott Aaronson, Quantum Computing Since Democritus (Cambridge University Press, 2013)
William J. Cook, In Pursuit of the Traveling Salesman: Mathematics at the Limits of Computation (Princeton University Press, 2012)
Lance Fortnow, The Golden Ticket: P, NP, and the Search for the Impossible (Princeton University Press, 2013)
Dennis Shasha, Out of their Minds: The Lives and Discoveries of 15 Great Computer Scientists (first published 1995; Springer, 2008)
Timothy Gowers at the University of Cambridge
Leslie Ann Goldberg at the University of Oxford
P versus NP problem - Wikipedia
P vs. NP for Dummies
Gödel’s Lost Letter and P=NP
MacTutor History of Mathematics archive
READING LIST:
Scott Aaronson, Quantum Computing Since Democritus (Cambridge University Press, 2013)
William J. Cook, In Pursuit of the Traveling Salesman: Mathematics at the Limits of Computation (Princeton University Press, 2012)
Lance Fortnow, The Golden Ticket: P, NP, and the Search for the Impossible (Princeton University Press, 2013)
Dennis Shasha, Out of their Minds: The Lives and Discoveries of 15 Great Computer Scientists (first published 1995; Springer, 2008)
Wikipedia Article Per Se
| Open problem in computer science:
If the answer to a problem is easy to check, is the problem itself easy to solve?
(more open problems in computer science) |
| Millennium Prize Problems |
|---|
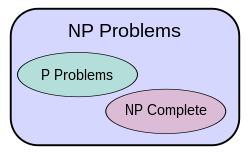
Diagram of complexity classes provided that P ≠ NP. The existence of problems within NP but outside both P and NP-complete, under that assumption, was established by Ladner's theorem.[1]
The informal term quickly, used above, means the existence of an algorithm for the task that runs in polynomial time. The general class of questions for which some algorithm can provide an answer in polynomial time is called "class P" or just "P". For some questions, there is no known way to find an answer quickly, but if one is provided with information showing what the answer is, it is possible to verify the answer quickly. The class of questions for which an answer can be verified in polynomial time is called NP.
Consider the subset sum problem, an example of a problem that is easy to verify, but whose answer may be difficult to compute. Given a set of integers, does some nonempty subset of them sum to 0? For instance, does a subset of the set {−2, −3, 15, 14, 7, −10} add up to 0? The answer "yes, because the subset {−2, −3, −10, 15} adds up to zero" can be quickly verified with three additions. However, there is no known algorithm to find such a subset in polynomial time (there is one, however, in exponential time, which consists of 2n-n-1 tries), but such an algorithm exists if P = NP; hence this problem is in NP (quickly checkable) but not necessarily in P (quickly solvable).
An answer to the P = NP question would determine whether problems that can be verified in polynomial time, like the subset-sum problem, can also be solved in polynomial time. If it turned out that P ≠ NP, it would mean that there are problems in NP (such as NP-complete problems) that are harder to compute than to verify: they could not be solved in polynomial time, but the answer could be verified in polynomial time.
Aside from being an important problem in computational theory, a proof either way would have profound implications for mathematics, cryptography, algorithm research, artificial intelligence, game theory, multimedia processing, philosophy, economics and many other fields.
Contents
[hide]- 1 Context
- 2 NP-complete
- 3 Harder problems
- 4 Problems in NP not known to be in P or NP-complete
- 5 Does P mean "easy"?
- 6 Reasons to believe P ≠ NP
- 7 Consequences of solution
- 8 Results about difficulty of proof
- 9 Claimed solutions
- 10 Logical characterizations
- 11 Polynomial-time algorithms
- 12 Formal definitions
- 13 Popular culture
- 14 See also
- 15 Notes
- 16 References
- 17 Further reading
- 18 External links
Context[edit]
The relation between the complexity classes P and NP is studied in computational complexity theory, the part of the theory of computation dealing with the resources required during computation to solve a given problem. The most common resources are time (how many steps it takes to solve a problem) and space (how much memory it takes to solve a problem).In such analysis, a model of the computer for which time must be analyzed is required. Typically such models assume that the computer is deterministic (given the computer's present state and any inputs, there is only one possible action that the computer might take) and sequential (it performs actions one after the other).
In this theory, the class P consists of all those decision problems (defined below) that can be solved on a deterministic sequential machine in an amount of time that is polynomial in the size of the input; the class NP consists of all those decision problems whose positive solutions can be verified in polynomial time given the right information, or equivalently, whose solution can be found in polynomial time on a non-deterministic machine.[5] Clearly, P ⊆ NP. Arguably the biggest open question in theoretical computer science concerns the relationship between those two classes:
- Is P equal to NP?
In 2012, 10 years later, the same poll was repeated. The number of researchers who answered was 151: 126 (83%) believed the answer to be no, 12 (9%) believed the answer is yes, 5 (3%) believed the question may be independent of the currently accepted axioms and therefore is impossible to prove or disprove, 8 (5%) said either don't know or don't care or don't want the answer to be yes nor the problem to be resolved.[7]
NP-complete[edit]
Main article: NP-complete
To attack the P = NP question, the concept of NP-completeness is very useful. NP-complete problems are a set of problems to each of which any other NP-problem can be reduced in polynomial time, and whose solution may still be verified in polynomial time. That is, any NP problem can be transformed into any of the NP-complete problems. Informally, an NP-complete problem is an NP problem that is at least as "tough" as any other problem in NP.NP-hard problems are those at least as hard as NP problems, i.e., all NP problems can be reduced (in polynomial time) to them. NP-hard problems need not be in NP, i.e., they need not have solutions verifiable in polynomial time.
For instance, the Boolean satisfiability problem is NP-complete by the Cook–Levin theorem, so any instance of any problem in NP can be transformed mechanically into an instance of the Boolean satisfiability problem in polynomial time. The Boolean satisfiability problem is one of many such NP-complete problems. If any NP-complete problem is in P, then it would follow that P = NP. Unfortunately, many important problems have been shown to be NP-complete, and not a single fast algorithm for any of them is known.
Based on the definition alone it is not obvious that NP-complete problems exist, a trivial and contrived NP-complete problem can be formulated as: given a description of a Turing machine M guaranteed to halt in polynomial time, does there exist a polynomial-size input that M will accept?[8] It is in NP because (given an input) it is simple to check whether M accepts the input by simulating M; it is NP-complete because the verifier for any particular instance of a problem in NP can be encoded as a polynomial-time machine M that takes the solution to be verified as input. Then the question of whether the instance is a yes or no instance is determined by whether a valid input exists.
The first natural problem proven to be NP-complete was the Boolean satisfiability problem. As noted above, this is the Cook–Levin theorem; its proof that satisfiability is NP-complete contains technical details about Turing machines as they relate to the definition of NP. However, after this problem was proved to be NP-complete, proof by reduction provided a simpler way to show that many other problems are also NP-complete, including the subset-sum problem discussed earlier. Thus, a vast class of seemingly unrelated problems are all reducible to one another, and are in a sense "the same problem".
Harder problems[edit]
See also: Complexity class
Although it is unknown whether P = NP, problems outside of P are known. A number of succinct problems (problems that operate not on normal input, but on a computational description of the input) are known to be EXPTIME-complete. Because it can be shown that P ⊊ EXPTIME, these problems are outside P, and so require more than polynomial time. In fact, by the time hierarchy theorem, they cannot be solved in significantly less than exponential time. Examples include finding a perfect strategy for chess (on an N × N board)[9] and some other board games.[10]The problem of deciding the truth of a statement in Presburger arithmetic requires even more time. Fischer and Rabin proved in 1974 that every algorithm that decides the truth of Presburger statements has a runtime of at least
 for some constant c. Here, n is the length of the Presburger statement. Hence, the problem is known to need more than exponential run time. Even more difficult are the undecidable problems, such as the halting problem. They cannot be completely solved by any algorithm, in the sense that for any particular algorithm there is at least one input for which that algorithm will not produce the right answer; it will either produce the wrong answer, finish without giving a conclusive answer, or otherwise run forever without producing any answer at all.
for some constant c. Here, n is the length of the Presburger statement. Hence, the problem is known to need more than exponential run time. Even more difficult are the undecidable problems, such as the halting problem. They cannot be completely solved by any algorithm, in the sense that for any particular algorithm there is at least one input for which that algorithm will not produce the right answer; it will either produce the wrong answer, finish without giving a conclusive answer, or otherwise run forever without producing any answer at all.Problems in NP not known to be in P or NP-complete[edit]
Main article: NP-intermediate
It was shown by Ladner that if P ≠ NP then there exist problems in NP that are neither in P nor NP-complete.[1] Such problems are called NP-intermediate problems. The graph isomorphism problem, the discrete logarithm problem and the integer factorization problem are examples of problems believed to be NP-intermediate. They are some of the very few NP problems not known to be in P or to be NP-complete.The graph isomorphism problem is the computational problem of determining whether two finite graphs are isomorphic. An important unsolved problem in complexity theory is whether the graph isomorphism problem is in P, NP-complete, or NP-intermediate. The answer is not known, but it is believed that the problem is at least not NP-complete.[11] If graph isomorphism is NP-complete, the polynomial time hierarchy collapses to its second level.[12][13] Since it is widely believed that the polynomial hierarchy does not collapse to any finite level, it is believed that graph isomorphism is not NP-complete. The best algorithm for this problem, due to Laszlo Babai and Eugene Luks has run time 2O(√nlog(n)) for graphs with n vertices.
The integer factorization problem is the computational problem of determining the prime factorization of a given integer. Phrased as a decision problem, it is the problem of deciding whether the input has a factor less than k. No efficient integer factorization algorithm is known, and this fact forms the basis of several modern cryptographic systems, such as the RSA algorithm. The integer factorization problem is in NP and in co-NP (and even in UP and co-UP[14]). If the problem is NP-complete, the polynomial time hierarchy will collapse to its first level (i.e., NP = co-NP). The best known algorithm for integer factorization is the general number field sieve, which takes expected time
Does P mean "easy"?[edit]
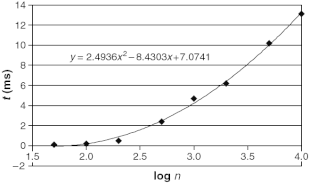
The graph shows time (average of 100 instances in ms using a 933 MHz Pentium III) vs.problem size for knapsack problems for a state-of-the-art specialized algorithm. Quadratic fit suggests that empirical algorithmic complexity for instances with 50–10,000 variables is O((log(n))2).[15]
First, it is not always true in practice. A theoretical polynomial algorithm may have extremely large constant factors or exponents thus rendering it impractical. On the other hand, even if a problem is shown to be NP-complete, and even if P ≠ NP, there may still be effective approaches to tackling the problem in practice. There are algorithms for many NP-complete problems, such as the knapsack problem, the traveling salesman problem and the Boolean satisfiability problem, that can solve to optimality many real-world instances in reasonable time. The empirical average-case complexity (time vs. problem size) of such algorithms can be surprisingly low. An example is the simplex algorithm in linear programming, which works surprisingly well in practice; despite having exponential worst-case time complexity it runs on par with the best known polynomial-time algorithms.[16]
Second, there are types of computations which do not conform to the Turing machine model on which P and NP are defined, such as quantum computation and randomized algorithms.
Reasons to believe P ≠ NP[edit]
According to polls,[6][17] many computer scientists believe that P ≠ NP. A key reason for this belief is that after decades of studying these problems no one has been able to find a polynomial-time algorithm for any of more than 3000 important known NP-complete problems (see List of NP-complete problems). These algorithms were sought long before the concept of NP-completeness was even defined (Karp's 21 NP-complete problems, among the first found, were all well-known existing problems at the time they were shown to be NP-complete). Furthermore, the result P = NP would imply many other startling results that are currently believed to be false, such as NP = co-NP and P = PH.It is also intuitively argued that the existence of problems that are hard to solve but for which the solutions are easy to verify matches real-world experience.[18]
If P = NP, then the world would be a profoundly different place than we usually assume it to be. There would be no special value in "creative leaps," no fundamental gap between solving a problem and recognizing the solution once it's found.On the other hand, some researchers believe that there is overconfidence in believing P ≠ NP and that researchers should explore proofs of P = NP as well. For example, in 2002 these statements were made:[6]
The main argument in favor of P ≠ NP is the total lack of fundamental progress in the area of exhaustive search. This is, in my opinion, a very weak argument. The space of algorithms is very large and we are only at the beginning of its exploration. [...] The resolution of Fermat's Last Theorem also shows that very simple questions may be settled only by very deep theories.
Being attached to a speculation is not a good guide to research planning. One should always try both directions of every problem. Prejudice has caused famous mathematicians to fail to solve famous problems whose solution was opposite to their expectations, even though they had developed all the methods required.
Consequences of solution[edit]
One of the reasons the problem attracts so much attention is the consequences of the answer. Either direction of resolution would advance theory enormously, and perhaps have huge practical consequences as well.P = NP[edit]
A proof that P = NP could have stunning practical consequences, if the proof leads to efficient methods for solving some of the important problems in NP. It is also possible that a proof would not lead directly to efficient methods, perhaps if the proof is non-constructive, or the size of the bounding polynomial is too big to be efficient in practice. The consequences, both positive and negative, arise since various NP-complete problems are fundamental in many fields.Cryptography, for example, relies on certain problems being difficult. A constructive and efficient solution[Note 1] to an NP-complete problem such as 3-SAT would break most existing cryptosystems including:
- public-key cryptography,[19] a foundation for many modern security applications such as secure financial transactions over the Internet; and
- symmetric ciphers such as AES or 3DES,[20] used for the encryption of communications data.
- one-way functions used in cryptographic hashing. The problem of finding a pre-image that hashes to a given value[21] must be difficult to be useful, and ideally should require exponential time. However, if P=NP, then finding a pre-image M can be done in polynomial time, through reduction to SAT.[22]
On the other hand, there are enormous positive consequences that would follow from rendering tractable many currently mathematically intractable problems. For instance, many problems in operations research are NP-complete, such as some types of integer programming and the travelling salesman problem. Efficient solutions to these problems would have enormous implications for logistics. Many other important problems, such as some problems in protein structure prediction, are also NP-complete;[23] if these problems were efficiently solvable it could spur considerable advances in life sciences and biotechnology.
But such changes may pale in significance compared to the revolution an efficient method for solving NP-complete problems would cause in mathematics itself. Gödel, in his early thoughts on computational complexity, noted that a mechanical method that could solve any problem would revolutionize mathematics:[24][25]
If there really were a machine with φ(n) ∼ k ⋅ n (or even ∼ k ⋅ n2), this would have consequences of the greatest importance. Namely, it would obviously mean that in spite of the undecidability of the Entscheidungsproblem, the mental work of a mathematician concerning Yes-or-No questions could be completely replaced by a machine. After all, one would simply have to choose the natural number n so large that when the machine does not deliver a result, it makes no sense to think more about the problem.Similarly, Stephen Cook says[26]
...it would transform mathematics by allowing a computer to find a formal proof of any theorem which has a proof of a reasonable length, since formal proofs can easily be recognized in polynomial time. Example problems may well include all of the CMI prize problems.Research mathematicians spend their careers trying to prove theorems, and some proofs have taken decades or even centuries to find after problems have been stated—for instance, Fermat's Last Theorem took over three centuries to prove. A method that is guaranteed to find proofs to theorems, should one exist of a "reasonable" size, would essentially end this struggle.
Donald Knuth has stated that he has come to believe that P = NP, but is reserved about the impact of a possible proof:[27]
[...] I don't believe that the equality P = N P will turn out to be helpful even if it is proved, because such a proof will almost surely be nonconstructive.
P ≠ NP[edit]
A proof that showed that P ≠ NP would lack the practical computational benefits of a proof that P = NP, but would nevertheless represent a very significant advance in computational complexity theory and provide guidance for future research. It would allow one to show in a formal way that many common problems cannot be solved efficiently, so that the attention of researchers can be focused on partial solutions or solutions to other problems. Due to widespread belief in P ≠ NP, much of this focusing of research has already taken place.[28]Also P ≠ NP still leaves open the average-case complexity of hard problems in NP. For example, it is possible that SAT requires exponential time in the worst case, but that almost all randomly selected instances of it are efficiently solvable. Russell Impagliazzo has described five hypothetical "worlds" that could result from different possible resolutions to the average-case complexity question.[29] These range from "Algorithmica", where P = NP and problems like SAT can be solved efficiently in all instances, to "Cryptomania", where P ≠ NP and generating hard instances of problems outside P is easy, with three intermediate possibilities reflecting different possible distributions of difficulty over instances of NP-hard problems. The "world" where P ≠ NP but all problems in NP are tractable in the average case is called "Heuristica" in the paper. A Princeton University workshop in 2009 studied the status of the five worlds.[30]
Results about difficulty of proof[edit]
Although the P = NP? problem itself remains open despite a million-dollar prize and a huge amount of dedicated research, efforts to solve the problem have led to several new techniques. In particular, some of the most fruitful research related to the P = NP problem has been in showing that existing proof techniques are not powerful enough to answer the question, thus suggesting that novel technical approaches are required.As additional evidence for the difficulty of the problem, essentially all known proof techniques in computational complexity theory fall into one of the following classifications, each of which is known to be insufficient to prove that P ≠ NP:
| Classification | Definition |
|---|---|
| Relativizing proofs | Imagine a world where every algorithm is allowed to make queries to some fixed subroutine called an oracle, and the running time of the oracle is not counted against the running time of the algorithm. Most proofs (especially classical ones) apply uniformly in a world with oracles regardless of what the oracle does. These proofs are called relativizing. In 1975, Baker, Gill, and Solovay showed that P = NP with respect to some oracles, while P ≠ NP for other oracles.[31] Since relativizing proofs can only prove statements that are uniformly true with respect to all possible oracles, this showed that relativizing techniques cannot resolve P = NP. |
| Natural proofs | In 1993, Alexander Razborov and Steven Rudich defined a general class of proof techniques for circuit complexity lower bounds, called natural proofs. At the time all previously known circuit lower bounds were natural, and circuit complexity was considered a very promising approach for resolving P = NP. However, Razborov and Rudich showed that, if one-way functions exist, then no natural proof method can distinguish between P and NP. Although one-way functions have never been formally proven to exist, most mathematicians believe that they do, and a proof or disproof of their existence would be a much stronger statement than the quantification of P relative to NP. Thus it is unlikely that natural proofs alone can resolve P = NP. |
| Algebrizing proofs | After the Baker-Gill-Solovay result, new non-relativizing proof techniques were successfully used to prove that IP = PSPACE. However, in 2008, Scott Aaronson and Avi Wigderson showed that the main technical tool used in the IP = PSPACE proof, known as arithmetization, was also insufficient to resolve P = NP.[32] |
These barriers have also led some computer scientists to suggest that the P versus NP problem may be independent of standard axiom systems like ZFC (cannot be proved or disproved within them). The interpretation of an independence result could be that either no polynomial-time algorithm exists for any NP-complete problem, and such a proof cannot be constructed in (e.g.) ZFC, or that polynomial-time algorithms for NP-complete problems may exist, but it's impossible to prove in ZFC that such algorithms are correct.[33] However, if it can be shown, using techniques of the sort that are currently known to be applicable, that the problem cannot be decided even with much weaker assumptions extending the Peano axioms (PA) for integer arithmetic, then there would necessarily exist nearly-polynomial-time algorithms for every problem in NP.[34] Therefore, if one believes (as most complexity theorists do) that not all problems in NP have efficient algorithms, it would follow that proofs of independence using those techniques cannot be possible. Additionally, this result implies that proving independence from PA or ZFC using currently known techniques is no easier than proving the existence of efficient algorithms for all problems in NP.
Claimed solutions [edit]
While the P versus NP problem is generally considered unsolved,[35] many amateur and some professional researchers have claimed solutions. Gerhard J. Woeginger has a comprehensive list.[36] An August 2010 claim of proof that P ≠ NP, by Vinay Deolalikar, a researcher at HP Labs, Palo Alto, received heavy Internet and press attention after being initially described as "seem[ing] to be a relatively serious attempt" by two leading specialists.[37] The proof has been reviewed publicly by academics,[38][39] and Neil Immerman, an expert in the field, had pointed out two possibly fatal errors in the proof.[40] In September 2010, Deolalikar was reported to be working on a detailed expansion of his attempted proof.[41] However, opinions expressed by several notable theoretical computer scientists indicate that the attempted proof is neither correct nor a significant advancement in the understanding of the problem.[42] This assessment prompted a May 2013 The New Yorker article to call the proof attempt "thoroughly discredited."[43]Logical characterizations[edit]
The P = NP problem can be restated in terms of expressible certain classes of logical statements, as a result of work in descriptive complexity.Consider all languages of finite structures with a fixed signature including a linear order relation. Then, all such languages in P can be expressed in first-order logic with the addition of a suitable least fixed-point combinator. Effectively, this, in combination with the order, allows the definition of recursive functions. As long as the signature contains at least one predicate or function in addition to the distinguished order relation, so that the amount of space taken to store such finite structures is actually polynomial in the number of elements in the structure, this precisely characterizes P.
Similarly, NP is the set of languages expressible in existential second-order logic—that is, second-order logic restricted to exclude universal quantification over relations, functions, and subsets. The languages in the polynomial hierarchy, PH, correspond to all of second-order logic. Thus, the question "is P a proper subset of NP" can be reformulated as "is existential second-order logic able to describe languages (of finite linearly ordered structures with nontrivial signature) that first-order logic with least fixed point cannot?".[44] The word "existential" can even be dropped from the previous characterization, since P = NP if and only if P = PH (as the former would establish that NP = co-NP, which in turn implies that NP = PH).
Polynomial-time algorithms[edit]
No algorithm for any NP-complete problem is known to run in polynomial time. However, there are algorithms for NP-complete problems with the property that if P = NP, then the algorithm runs in polynomial time (although with enormous constants, making the algorithm impractical). The following algorithm, due to Levin (without any citation), is such an example below. It correctly accepts the NP-complete language SUBSET-SUM. It runs in polynomial time if and only if P = NP:// Algorithm that accepts the NP-complete language SUBSET-SUM.
//
// this is a polynomial-time algorithm if and only if P = NP.
//
// "Polynomial-time" means it returns "yes" in polynomial time when
// the answer should be "yes", and runs forever when it is "no".
//
// Input: S = a finite set of integers
// Output: "yes" if any subset of S adds up to 0.
// Runs forever with no output otherwise.
// Note: "Program number P" is the program obtained by
// writing the integer P in binary, then
// considering that string of bits to be a
// program. Every possible program can be
// generated this way, though most do nothing
// because of syntax errors.
FOR N = 1...∞
FOR P = 1...N
Run program number P for N steps with input S
IF the program outputs a list of distinct integers
AND the integers are all in S
AND the integers sum to 0
THEN
OUTPUT "yes" and HALT
If, and only if, P = NP, then this is a polynomial-time algorithm accepting an NP-complete language. "Accepting" means it gives "yes" answers in polynomial time, but is allowed to run forever when the answer is "no" (also known as a semi-algorithm).This algorithm is enormously impractical, even if P = NP. If the shortest program that can solve SUBSET-SUM in polynomial time is b bits long, the above algorithm will try at least 2b−1 other programs first.
Formal definitions[edit]
P and NP[edit]
Conceptually speaking, a decision problem is a problem that takes as input some string w over an alphabet Σ, and outputs "yes" or "no". If there is an algorithm (say a Turing machine, or a computer program with unbounded memory) that can produce the correct answer for any input string of length n in at most cnk steps, where k and c are constants independent of the input string, then we say that the problem can be solved in polynomial time and we place it in the class P. Formally, P is defined as the set of all languages that can be decided by a deterministic polynomial-time Turing machine. That is,- M halts on all input w and
- there exists
 such that
such that  , where O refers to the big O notation and
, where O refers to the big O notation and
Let L be a language over a finite alphabet, Σ.
L ∈ NP if, and only if, there exists a binary relation
 and a positive integer k such that the following two conditions are satisfied:
and a positive integer k such that the following two conditions are satisfied:- For all
 ,
,  such that (x, y) ∈ R and
such that (x, y) ∈ R and  ; and
; and - the language
 over
over  is decidable by a Turing machine in polynomial time.
is decidable by a Turing machine in polynomial time.
In general, a verifier does not have to be polynomial-time. However, for L to be in NP, there must be a verifier that runs in polynomial time.
Example[edit]
LetCOMPOSITE also happens to be in P.[45][46]
NP-completeness[edit]
There are many equivalent ways of describing NP-completeness.Let L be a language over a finite alphabet Σ.
L is NP-complete if, and only if, the following two conditions are satisfied:
- L ∈ NP; and
- any L′ in NP is polynomial-time-reducible to L (written as
 ), where
), where  if, and only if, the following two conditions are satisfied:
if, and only if, the following two conditions are satisfied: - There exists f : Σ* → Σ* such that for all w in Σ* we have:
 ; and
; and - there exists a polynomial-time Turing machine that halts with f(w) on its tape on any input w.
- There exists f : Σ* → Σ* such that for all w in Σ* we have:
Popular culture[edit]
- The film Travelling Salesman, by director Timothy Lanzone, is the story of four mathematicians hired by the US government to solve the P vs. NP problem.[47]
See also[edit]
- Game complexity
- Unique games conjecture
- Unsolved problems in computer science
- Unsolved problems in mathematics
Notes[edit]
- Jump up ^ Exactly how efficient a solution must be to pose a threat to cryptography depends on the details. A solution of
 or better and a reasonable constant term would be disastrous. On the other hand, a solution that is
or better and a reasonable constant term would be disastrous. On the other hand, a solution that is 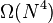 or worse in almost all cases would not pose an immediate practical danger.
or worse in almost all cases would not pose an immediate practical danger.
References[edit]
- ^ Jump up to: a b R. E. Ladner "On the structure of polynomial time reducibility," Journal of the ACM, 22, pp. 151–171, 1975. Corollary 1.1. ACM site.
- Jump up ^ Juris. "Gödel, von Neumann, and the P = NP problem" (PDF). Bulletin of the European Association for Theoretical Computer Science 38: 101–107.
- Jump up ^ Cook, Stephen (1971). "The complexity of theorem proving procedures". Proceedings of the Third Annual ACM Symposium on Theory of Computing. pp. 151–158.
- Jump up ^ Fortnow, Lance (2009). "The status of the P versus NP problem" (PDF). Communications of the ACM 52 (9): 78–86. doi:10.1145/1562164.1562186.
- Jump up ^ Sipser, Michael: Introduction to the Theory of Computation, Second Edition, International Edition, page 270. Thomson Course Technology, 2006. Definition 7.19 and Theorem 7.20.
- ^ Jump up to: a b c William I. Gasarch (June 2002). "The P=?NP poll." (PDF). SIGACT News 33 (2): 34–47. doi:10.1145/1052796.1052804. Retrieved 29 December 2008.
- Jump up ^ William I. Gasarch. "The Second P=?NP poll" (PDF). SIGACT News 74.
- Jump up ^ Scott Aaronson. "PHYS771 Lecture 6: P, NP, and Friends". Retrieved 27 August 2007.
- Jump up ^ Aviezri Fraenkel and D. Lichtenstein (1981). "Computing a perfect strategy for n×n chess requires time exponential in n". J. Comb. Th. A (31): 199–214.
- Jump up ^ David Eppstein. "Computational Complexity of Games and Puzzles".
- Jump up ^ Arvind, Vikraman; Kurur, Piyush P. (2006). "Graph isomorphism is in SPP". Information and Computation 204 (5): 835–852. doi:10.1016/j.ic.2006.02.002.
- Jump up ^ Schöning, Uwe. "Graph isomorphism is in the low hierarchy". Proceedings of the 4th Annual Symposium on Theoretical Aspects of Computer Science 1987: 114–124. doi:10.1007/bfb0039599.
- Jump up ^ Schöning, Uwe (1988). "Graph isomorphism is in the low hierarchy". Journal of Computer and System Sciences 37: 312–323. doi:10.1016/0022-0000(88)90010-4.
- Jump up ^ Lance Fortnow. Computational Complexity Blog: Complexity Class of the Week: Factoring. 13 September 2002.
- Jump up ^ Pisinger, D. 2003. "Where are the hard knapsack problems?" Technical Report 2003/08, Department of Computer Science, University of Copenhagen, Copenhagen, Denmark
- Jump up ^ Gondzio, Jacek; Terlaky, Tamás (1996). "3 A computational view of interior point methods". In J. E. Beasley. Advances in linear and integer programming. Oxford Lecture Series in Mathematics and its Applications 4. New York: Oxford University Press. pp. 103–144. MR 1438311. Postscript file at website of Gondzio and at McMaster University website of Terlaky.
- Jump up ^ Rosenberger, Jack (May 2012). "P vs. NP poll results". Communications of the ACM 55 (5): 10.
- Jump up ^ Scott Aaronson. "Reasons to believe"., point 9.
- Jump up ^ See Horie, S. and Watanabe, O.; Watanabe (1997). "Hard instance generation for SAT". Algorithms and Computation. Lecture Notes in Computer Science (Springer) 1350: 22–31. arXiv:cs/9809117. Bibcode:1998cs........9117H. doi:10.1007/3-540-63890-3_4. ISBN 978-3-540-63890-2. for a reduction of factoring to SAT. A 512 bit factoring problem (8400 MIPS-years when factored) translates to a SAT problem of 63,652 variables and 406,860 clauses.
- Jump up ^ See, for example, Massacci, F. and Marraro, L. (2000). "Logical cryptanalysis as a SAT problem". Journal of Automated Reasoning (Springer) 24 (1): 165–203. doi:10.1023/A:1006326723002. CiteSeerX: 10
.1 .1 .104 .962. in which an instance of DES is encoded as a SAT problem with 10336 variables and 61935 clauses. A 3DES problem instance would be about 3 times this size. - Jump up ^ Find a messageM that when hashed by the function H() gives a digest h, or H(M)=h
- Jump up ^ De, Debapratim and Kumarasubramanian, Abishek and Venkatesan, Ramarathnam (2007). "Inversion attacks on secure hash functions using SAT solvers". Springer. pp. 377–382.
- Jump up ^ Berger B, Leighton T (1998). "Protein folding in the hydrophobic-hydrophilic (HP) model is NP-complete". J. Comput. Biol. 5 (1): 27–40. doi:10.1089/cmb.1998.5.27. PMID 9541869.
- Jump up ^ History of this letter and its translation from Michael Sipser. "The History and Status of the P versus NP question" (PDF).
- Jump up ^ David S. Johnson. "A Brief History of NP-Completeness, 1954–2012" (PDF). From pages 359–376 of Optimization Stories, M. Grötschel (editor), a special issue of ¨ Documenta Mathematica, published in August 2012 and distributed to attendees at the 21st International Symposium on Mathematical Programming in Berlin.
- Jump up ^ Cook, Stephen (April 2000). "The P versus NP Problem" (PDF). Clay Mathematics Institute. Retrieved 18 October 2006.
- Jump up ^ Knuth, Donald E. (May 20, 2014). "Twenty Questions for Donald Knuth". informit.com. InformIT. Retrieved 20 July 2014.
- Jump up ^ L. R. Foulds (October 1983). "The Heuristic Problem-Solving Approach". Journal of the Operational Research Society 34 (10): 927–934. doi:10.2307/2580891. JSTOR 2580891.
- Jump up ^ R. Impagliazzo, "A personal view of average-case complexity," sct, pp.134, 10th Annual Structure in Complexity Theory Conference (SCT'95), 1995
- Jump up ^ "Tentative program for the workshop on "Complexity and Cryptography: Status of Impagliazzo's Worlds"". Archived from the original on 2013-11-15.
- Jump up ^ T. P. Baker, J. Gill, R. Solovay. Relativizations of the P =? NP Question. SIAM Journal on Computing, 4(4): 431–442 (1975)
- Jump up ^ S. Aaronson and A. Wigderson (2008). Algebrization: A New Barrier in Complexity Theory (PDF). Proceedings of ACM STOC'2008. pp. 731–740. doi:10.1145/1374376.1374481.
- Jump up ^ Aaronson, Scott. "Is P Versus NP Formally Independent?" (PDF).
- Jump up ^ Ben-David, Shai; Halevi, Shai (1992). "On the independence of P versus NP". Technical Report 714. Technion.
- Jump up ^ John Markoff (8 October 2009). "Prizes Aside, the P-NP Puzzler Has Consequences". The New York Times.
- Jump up ^ Gerhard J. Woeginger. "The P-versus-NP page". Retrieved 25 May 2014.
- Jump up ^ Markoff, John (16 August 2010). "Step 1: Post Elusive Proof. Step 2: Watch Fireworks.". The New York Times. Retrieved 20 September 2010.
- Jump up ^ Polymath Project wiki. "Deolalikar's P vs NP paper".
- Jump up ^ Science News, "Crowdsourcing peer review"
- Jump up ^ Dick Lipton (12 August 2010). "Fatal Flaws in Deolalikar's Proof?".
- Jump up ^ Dick Lipton (15 September 2010). "An Update on Vinay Deolalikar's Proof". Retrieved 31 December 2010.
- Jump up ^ Gödel’s Lost Letter and P=NP, Update on Deolalikar’s Proof that P≠NP
- Jump up ^ Alexander Nazaryan (2 May 2013). "A Most Profound Math Problem". Retrieved 1 May 2014.
- Jump up ^ Elvira Mayordomo. "P versus NP" Monografías de la Real Academia de Ciencias de Zaragoza 26: 57–68 (2004).
- Jump up ^ M. Agrawal, N. Kayal, N. Saxena. "Primes is in P" (PDF). Retrieved 29 December 2008.
- Jump up ^ AKS primality test
- Jump up ^ Geere, Duncan. "'Travelling Salesman' movie considers the repercussions if P equals NP". Wired. Retrieved 26 April 2012.
Further reading[edit]
- Fraenkel, A. S.; Lichtenstein, D. "Computing a Perfect Strategy for n*n Chess Requires Time Exponential in N.". doi:10.1007/3-540-10843-2+23.
- Garey, Michael; Johnson, David (1979). Computers and Intractability: A Guide to the Theory of NP-Completeness. San Francisco: W. H. Freeman and Company. ISBN 0-7167-1045-5.
- Goldreich, Oded (2010). P, Np, and Np-Completeness. Cambridge: Cambridge University Press. ISBN 978-0-521-12254-2. Online drafts
- Immerman, N. (1987). "Languages which capture complexity classes". SIAM Journal of Computing 16 (4): 760–778. doi:10.1137/0216051.
- Cormen, Thomas (2001). Introduction to Algorithms. Cambridge: MIT Press. ISBN 0-262-03293-7.
- Papadimitriou, Christos (1994). Computational Complexity. Boston: Addison-Wesley. ISBN 0-201-53082-1.
- Fortnow, L. (2009). "The Status of the P versus NP problem". Communications of the ACM 52 (9): 78. doi:10.1145/1562164.1562186.
- Fortnow, L.; Gasarch, W. "Computational complexity".
- Fortnow, Lance. The Golden Ticket: P, NP, and the Search for the Impossible ISBN 9780691156491. Princeton University Press. Princeton, NJ (2013)
External links[edit]
This audio file was created from a revision of the "P versus NP problem" article dated 2013-08-12, and does not reflect subsequent edits to the article. (Audio help)
- The Clay Mathematics Institute Millennium Prize Problems
- The Clay Math Institute Official Problem Description PDF (118 KB)
- Gerhard J. Woeginger. The P-versus-NP page. A list of links to a number of purported solutions to the problem. Some of these links state that P equals NP, some of them state the opposite. It is probable that all these alleged solutions are incorrect.
- Scott Aaronson 's Shtetl Optimized blog: Reasons to believe, a list of justifications for the belief that P ≠ NP
| ||||||||||||||||||||||


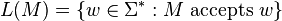

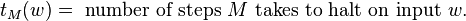


No comments:
Post a Comment